CS180: Introduction to Computer Vision & Computation Photography

Project 3

Face Morphing

Clara Hung

Project Overview

The goal of this project is to use what we've learned about transformations to create a morph animation of our face into someone else's face. Additionally, we'll compute the mean of a population of faces and extrapolate from a mean to make a caricature of ourselves.

Part 1: Defining Correspondances

For this part, I first defined 55 corresponding points on my two images by hand, including 4 points that represent the 4 corners of the image so we can morph the background as well. At first, I wrote my on tool using ginput, but it was inconvinient to remember the ordering of my points, so I used this correspondance tool from last year to define my points. The key here is to make sure that the points on the two faces are in the same order. I saved these points as a json to make my life easier.

Next, in order to actually do the morph, we need a triangulation. I used a Delaunay triangulation because that is the most optimal for morphing since it doesn't produce triangles with extreme angles (too big or too small). We like it "just right" just like goldilocks. To make my morph look better, I first computed the a set of midpoints by taking the average of corresponding points. This makes the morph look more gradual and pleasing to the eye. Then, I used scipy's Delaunay class to compute the triangulations at the midway shape.

Below are images if my midway triangulation displayed on both of my test faces! I tried besties Taylor Swift and Karlie Kloss from Martin Schoeller's collection. It also makes my life easier since they have similar faces : ).

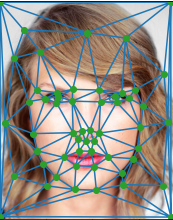
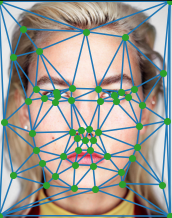
Part 2: Computing the "Mid-Way Face"

Before computing the whole morph sequence, we compute the midway face as a benchmark to make sure our code works, and we can use it to build the full morph sequence. To compute the mid-way face, we must complete the following steps:

1. Compute the average shape of the two faces by taking the average of the corresponding points.
2. Compute the Delaunay triangulation of the average shape.
3. For each triangle: Compute the affine transformation matrices for each triangle in the triangulation for both faces. This matrix transforms FROM the image TO the midway face.
4. Take the inverse affine matrix.
5. Apply the inverse affine transformation matrices from the midway face TO the original image and use this to interpolate the color values of that triangle (aka, paint the patch).
6. Repeat for all triangles. Add each result to our final midway face.
7. Compute the mid-way face by taking the average of the two warped faces.

Here are my results!

I also did a midway morph of me and my friend Janet! We took some fancy headshots at an Astronaut Scholars Event.

Part 3: The Morph Sequence

To produce the morph sequence, I can use the code I wrote above but adapt it with two new parameters: warp_frac and dissolve_frac. These control how much we warp and cross-dissolve, respectively, and they should both be proportional to which "frame" we are in. mathematically, this looks like a weighted average: \( (1 - \alpha) \cdot \text{img1} + \alpha \cdot \text{img2} \). For my results below, I used 50 frames at 30fps.

Part 4: The "Mean Face" of a Population

Now, we want to get a very mean face... in the mathematical sense! I took the FEI dataset because it was the easiest to work with, corresponding points wise. I wish I was more creative and actually found an Asian person database to use, but alas, I have grad apps to work on and don't have time to go digging :'). This dataset consists of 200 individuals take at the AI Laboratory of FEI in Bernardo do Campo, São Paulo, Brazil. There are 1000 male and 1000 female subjects, with one neutral photo and one smiling photo. They come with 46 annotated correspondance points, which is what we'll be using to compute the mean face!

To compute the mean face, we first choose a subset of the data: neutral or smiling. For each subset, we compute the average of each point across all 1000 images. Then, using this point set, we create a triangulation, warp each face to this "mean face", and average all the warped faces. Make sure you used the normalized data provided on the website! This way, all the faces are already aligned for you! I had to make sure my code could work with grayscale images for this part.

Here are my results!

Here are some examples of Brazilians morphed to the average face:

Ever wonder what I look like as a Brazilian? Never? Me neither. However, CS180 staff wants to see it so here it goes... To do this, I first had to find a photo that roughly matches the photos they had. Then, I had to resize and downsample to match the dimensions. Then, I had to annotate all 46 points, in-order, for my own photo. To warp to the average Brazilian, I warped myself to the mean triangulation. To clara-fy the Brazilians, I had to warp them to my triangulation.

My images look kind of funky, and I think it's because I couldn't find an image that had the right aspect ratio and perspective as the Brazilian images. I don't think you want a photo of my as I am writing this, so apologies that this will have to do. I think the results would end up better if I used the image alignment code from project 2 to align the images together.

Part 5: Caricatures: Extrapolating From the Mean

Now, we want to make a caricature of myself -- oh my! To do this, we first compute the difference between the mean face and the original face. Then, we multiply this difference by a scalar \( \alpha \) to get a caricature. Mathematically, this looks like: \((1 - \alpha) \cdot \text{self} + \alpha \cdot \text{mean}\). This scalar can be positive or negative, depending on if you want to exaggerate or minimize the features. I chose to use \( \alpha = 0.5 \) for my results, which means this is the image we get when we exaggerate my face's features. We can see that it makes my face a lot more pentagonal since my face is already pretty pentagonal.

Part 6: Bells and Whistles

For my bells and whistles, I thought it would be cool to morph my siblings and I together! For this, I first aligned ourselves using the alignment code from Project 2, selected 50 key points, and followed the process outlined in part 2 and 3. There's some aliasing in the colors. I think it might be due to not normalizing my images first. The video is created using 60 frames of morphs! The music I chose has a flute piece because my youngest brother loves flute. If the video below doesn't work, you can also access it here.